С 22 по 27 января в нашей школе прошла Неделя математики. В течение недели детям не раз пришлось проявить математическую смекалку при решении «хитрых» задач, демонстрировать свои знания по разным темам, испытать свои силы в различных видах деятельности.
Неделя началась с торжественной линейки, после которой учащиеся представили себя и свой класс в числах, показали свои знания по математике в ходе занимательных викторин и решения математических кроссвордов. Ребята показали, что умеют нестандартно мыслить, логически рассуждать.
В конце первого дня школьники получили домашнее задание, а во вторник приняли участие в математическом флешмобе «В математике правят цифры».
На третий день в старших классах прошла квест-игра «В поисках истины». Юные математики дружно работали в командах, помогали друг другу, обсуждали трудные вопросы, переживали за своих товарищей. Все учащиеся с заданиями справлялись быстро и получали соответствующие баллы. Конкурсы получились интересными и увлекательными. День прошел здорово и весело!
В четверг ребята 7 и 8 классов участвовали в интерактивной игре «Час весёлой математики», учащиеся начальной школы — в «Математической викторине».
В пятницу была проведена игра «Математическое Поле-Чудес», на котором школьники отгадывали фамилии знаменитых математиков.
В конце праздника, на торжественном закрытии Недели математики, были подведены итоги. Тем учащимся, которые особенно отличились на протяжении недели, вручили грамоты, дипломы и сладкие подарки.
Неделя пробежала быстро. Её итогом стало множество побед, открытий и свершений. Мы ещё раз убедились в том, что МАТЕМАТИКА – Царица наук, а мы – жители этого царства. Спасибо всем участникам!



















 1)Сколько квадратных метров листовой жести пойдёт на изготовление 4-ёх водосточных трубы для дачного домика, если длина трубы 5 м и диаметр 10 см ? На отходы и швы нужно добавить 5%.
1)Сколько квадратных метров листовой жести пойдёт на изготовление 4-ёх водосточных трубы для дачного домика, если длина трубы 5 м и диаметр 10 см ? На отходы и швы нужно добавить 5%. Задача 1. В связи с инфляцией происходит ежегодная индексация пенсий в среднем на 5% в год. Какую пенсию будет получать пенсионер через 3 года, если в этом году она составляет 15 000 рублей?
Задача 1. В связи с инфляцией происходит ежегодная индексация пенсий в среднем на 5% в год. Какую пенсию будет получать пенсионер через 3 года, если в этом году она составляет 15 000 рублей?
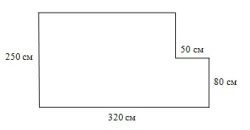

 В начале лета можно позволить детям почувствовать полную свободу, разрешить побездельничать неделю-другую. Ведь каникулы — лучшее время заняться любимыми делами, получить новые впечатления.
В начале лета можно позволить детям почувствовать полную свободу, разрешить побездельничать неделю-другую. Ведь каникулы — лучшее время заняться любимыми делами, получить новые впечатления.